Depending on the angle of the rotation and its location on the curve, these amazing patterns get created. The growth is linear; expanding by one module with each step. Physical reality is much more than surfaces on a screen therefore students created complex parametric models working as systems linked to many forces gravity, environment, structure…etc… and not just finished objects. If you have any questions on one of the images, please do not hesitate to ask. Below are most of the printscreens that I used to help the students with their journey into parametric modelling which is based on help that I also received previously. One of our main ambitions was to link physical and digital experiments so that one feeds the other. 
| Uploader: | Nikozuru |
| Date Added: | 6 July 2008 |
| File Size: | 61.53 Mb |
| Operating Systems: | Windows NT/2000/XP/2003/2003/7/8/10 MacOS 10/X |
| Downloads: | 77905 |
| Price: | Free* [*Free Regsitration Required] |
Tag: hoopsnake
Simply by double clicking on the Hoopsnake component in the definition and then adjust the preferable angles and click loop. The two examples are based on a cube and a tetrahedron.

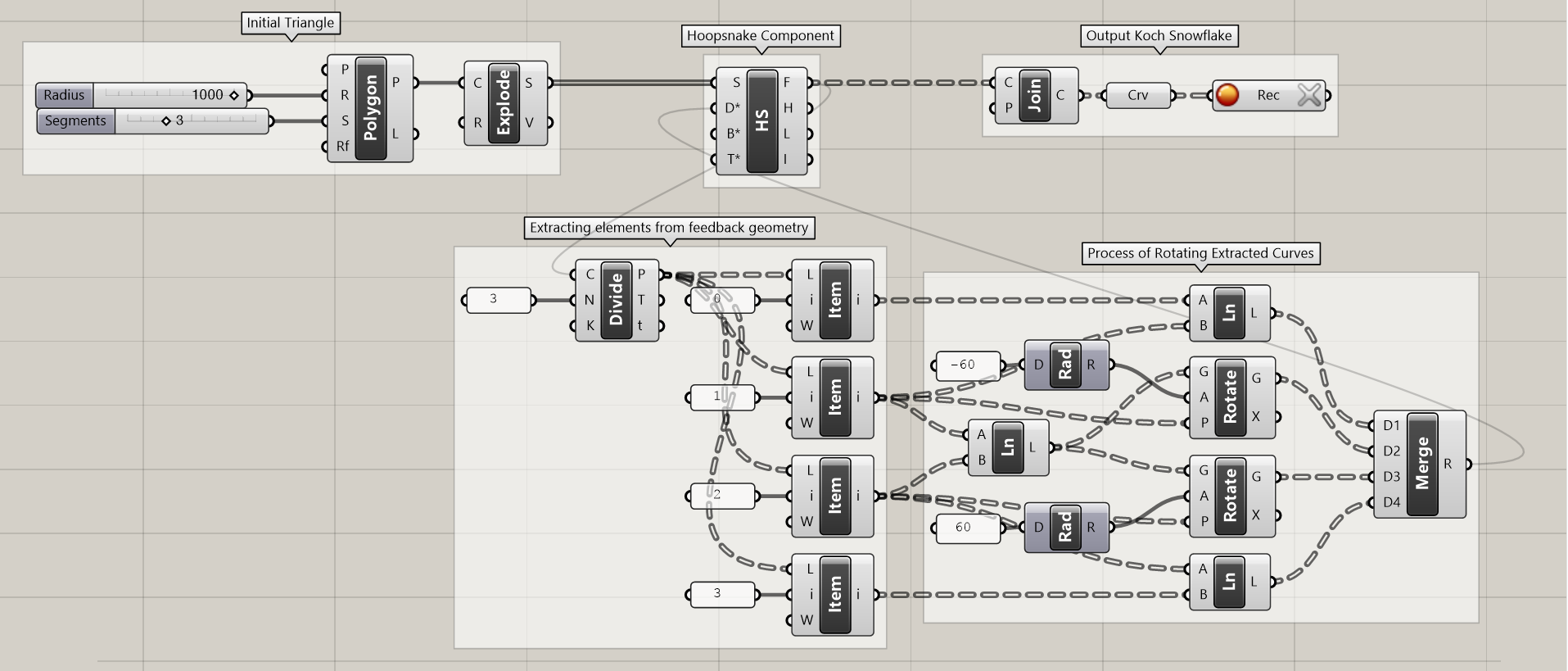
A line rotates on hoopxnake line and this new line becomes the currrent one on which the rotation is done and so one and so forth. Progression of a Koch snowflake as it is described by a recursive definition I wrote in grasshopper. Below is my favourite image: The position of each new module is determined by a new randomly selected face of the preceding module.
Koch tetrahedron Paper model for Koch tetrahedron Paper model. The video indicates how you do it. If you have any questions on one of the images, please do not hesitate to ask.
The second video is a very simple example of recursion using Hoopsnake by Volatile Prototype for Grasshopper: Below are most of the printscreens that I used to help the students with their journey into parametric modelling which is based on help that I also received previously. It was done with Grasshopper and the free Kangaroo plugin by Daniel Piker.
Physical reality is much more than surfaces on a screen therefore students created complex parametric models working as systems linked to many forces gravity, environment, structure…etc… and not just finished objects. One of our main ambitions grassnopper to link physical and digital experiments so that one feeds the other. Application of the same principle for a regular tetrahedron made through a recursive hrasshopper definition.
Depending on the angle of the rotation and its location on the curve, these amazing patterns get created. You can repeat the operation as many times as you want with different variation of angles and once the satisfied result is there you can bake the meshes into Rhino and then use them to render. The growth is linear; expanding by one module with each step.
To do so, they used Grasshopper and its numerous plugins provided by generous developers. The first video shows the trail left by points constrained by springs, end points and gravity.
hoopsnake –
I hope that this will help others to design amazing things! These very precise digital models allow students to implement what they learn from their physical models, to simulate even more design options and further understand the rules behind them.
The Arch moves up and to the side, leaving a beautiful trace which reminded me of the pictures of Edouard Muybridge. Grasshopper is a graphical algorithm editor integrated with Rhinoceros 3D modelling tool and a 18, strong community exchanging ideas and helping each other on the Grasshopper3d.
Boids behaviour with Hoopsnake. Progression of a Koch snowflake as it is described by a recursive definition I wrote in grasshopper Koch snowflake in Grasshopper Application of the same principle hoopsnkae a regular tetrahedron made through a recursive hrasshopper definition.

No comments:
Post a Comment